Beta Regression in Python
A little background
I had a reason recently to run a beta regression and spent a little bit of time getting it up and running in Python. At the time the latest release candidate for statsmodels, with a newly added implementation of beta regression, wasn’t released, so I had to make do with running R from Python. To be specific, what I wanted was to investigate model predictions by running a cross-validated beta regression. What I really wanted was to have everything running in Python but have the reliability of a beta regression package that had been out in the wild for a while with all the issues ironed out. That’s generally the dream - take any functionality that’s only available in R or another language and get it running in Python. This post will go through the basics of this with some sample code for getting it all up and running.
Beta regression
First though, a valid question - what’s a beta regression? It’s a regression that assumes our outcome is beta distributed, which makes it appropriate for values in the open interval (0, 1) (i.e. they can’t actually be 0 or 1) such as rates, fractions, probabilities. The PDF for different values of alpha and beta, which parameterise the beta distribution, is shown below.
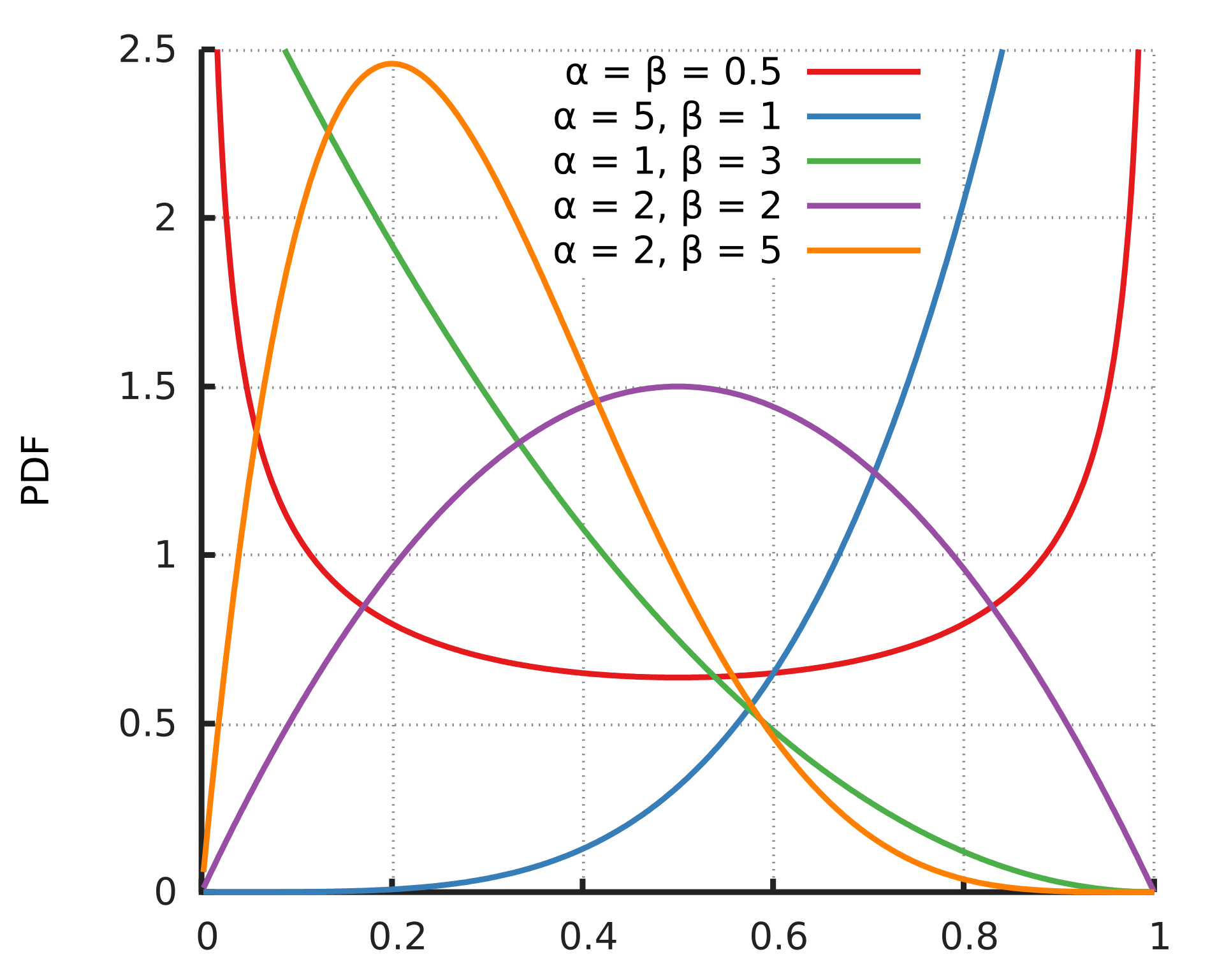The beta distribution PDF, lifted from wikipedia
As all the models I was using had been recalibrated using Platt scaling, this is what I had to work with. I also had predictions from a single model, rather than from each fold of cross-validation. This is nice as I could avoid the issue of having to running my cross-validated beta regression separately for each test fold, as model predictions from CV cannot just be combined. Before getting started I did hesitate as my instinct was to think that I could get a logistic regression to run as if my outcome were fractions and work the model this way. This answer on cross-validated helped assuage my worries, and I ultimately ran both but found much better prediction from the beta regression. This makes sense as it’s much more flexible and can use different link functions, including logistic. More information on beta regression itself is available in the 2004 paper by Ferrari and Cribari-Neto and in the vignette for the R package I used, betareg.
Calling betareg from Python
So assuming that, like me, beta regression is the thing you need, calling it from Python is surpisingly easy using the rpy2 package. First, load the requirements below which will take care of everything we do later.
import rpy2.robjects as ro
from rpy2.objects import pandas2ri
from rpy2.robjects.packages import importr
from rpy2.robjects.conversion import localconverter
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
from functools import reduce
Next we can setup a basic function in R to run a beta regression and return effect sizes and predictions in the test set, like below:
breg = importr('betareg')
ro.r('''
beta_regression <- function(train, test, formula) {
# run and store beta regression results
blm <- betareg(as.formula(formula), data=train)
output <- list("y_pred" = predict(blm, test),
"beta" = coef(blm))
return(output)
}''')
beta_regression = ro.globalenv['beta_regression']
And now we just need to call this while converting data to be handled by R. This is most easily done using a with statement
with localconverter(ro.default_converter + pandas2ri.converter):
prediction, betas, r2, ll = beta_regression(train, test, r_formula)
where the r_formula is the standard ‘y ~ x1 + x2’ notation for a glm in R. And now we have beta regression running in R! Originally I had a few more things being returned from this function, because I wanted p-values and standard errors, but I was looking at a pretty big dataset and this was causing a memory blow-up on the HPC cluster I couldn’t solve quickly.
Cross-validation (CV)
Stepping things up a little, we might want to cross-validate our beta regression. One thing we could do is build a sklearn-compatible classifier so it can be used in pipelines. Right now I’m more interested in getting this off the ground than releasing a sklearn version for use (though I might do that soon!) so I’ve just manually set up basic CV and scaling. Incorporating the code from above, this gives us the function below, which can be called with one or more predictors. Yay! Note that I’ve got the notation of the outcome being labelled y_pred by default because I was using the model to see how well variables predicted model predictions (it makes sense, I swear). Unless you’re also after this niche then y_name will be whatever your outcome is called.
def beta_regression_cv(data, X_name, y_name='y_pred', seed=12345, cv=5, shuffle=True,
scale=True, verbose=True):
breg = importr('betareg')
ro.r('''
beta_regression <- function(train, test, formula) {
# run and store beta regression results
blm <- betareg(as.formula(formula), data=train)
output <- list("y_pred" = predict(blm, test),
"beta" = coef(blm))
return(output)
}''')
beta_regression = ro.globalenv['beta_regression']
fold = KFold(cv, shuffle=shuffle, random_state=seed)
cv_folds, y_pred, y_true, indices = [], [], [], []
cv_models = pd.DataFrame({})
if not isinstance(X_name, (list, tuple)):
X_name = [X_name]
data = data.dropna(subset=X_name)
obs = data.shape[0]
X = data.loc[:, X_name].copy()
y = data.loc[:, y_name].copy()
del data
r_formula = y_name + ' ~ ' + ' + '.join(X_name)
if verbose:
print('Running Beta Regression with formula {} on training data of shape {}'.format(r_formula, X.shape))
for n_fold, (train, test) in enumerate(fold.split(X, y)):
X_ = X.copy()
if isinstance(X_, pd.Series):
X_ = X_.to_frame()
X_train, y_train = X_.iloc[train, :], y.iloc[train]
X_test, y_test = X_.iloc[test, :], y.iloc[test]
indices.append(X_test.index.values)
if scale:
std_scaler = StandardScaler()
train = pd.DataFrame(std_scaler.fit_transform(X_train), index=X_train.index,
columns=X_train.columns)
test = pd.DataFrame(std_scaler.transform(X_test), index=X_test.index,
columns=X_test.columns)
else:
train = X_train
test = X_test
train[y_name] = y_train
test[y_name] = y_test
with localconverter(ro.default_converter + pandas2ri.converter):
prediction, betas, r2, ll = beta_regression(train, test, r_formula)
model = (pd.DataFrame({'estimate': betas})
.assign(variable=['intercept'] + X_name + ['Phi'],
fold=n_fold))
cv_models = model if n_fold == 0 else cv_models.append(model)
y_pred.append(prediction)
y_true.append(y_test.copy())
cv_folds.append(np.repeat(n_fold, len(y_pred[n_fold])))
cv_predictions = pd.DataFrame({'y_pred': np.hstack(y_pred), 'y_true': np.hstack(y_true),
'fold': np.hstack(cv_folds), 'obs': obs,
'formula': r_formula, 'outcome': y_name,
'ids': np.hstack(indices)})
return cv_predictions, cv_models.assign(obs=obs, formula=r_formula, outcome=y_name, predictors=str(X_name))
Cross-validation for any number of predictions and outcomes
This little issue might be more specific to me, but I’ll leave it here in case it’s useful. What I needed beyond this was to get the mean test fold R2 when checking multiple predictors and multiple outcomes. Because the first function is nice and simple we can just add a couple more to handle this behaviour. The function below applies any nuumber of predictors against a single outcome. So, for example, you could pass ['age', 'sex', 'height', ['age', 'sex', 'height']], to check how well each of the predictors does alone compared to together in multivariable regression.
def r2_by_predictor(data, predictor_names, y_name, scale=True, cv=5, shuffle=True):
correlations, predictions, models = [], [], []
X_names = [p if isinstance(p, list) else [p] for p in predictor_names]
for i, p in enumerate(predictor_names):
beta_results, beta_models = beta_regression_cv(data, X_name=p, y_name=y_name, scale=scale, cv=cv,
shuffle=shuffle)
g = (beta_results.groupby('fold')
.apply(lambda x: r2_score(x['y_true'], x['y_pred']))
.to_frame()
.rename(columns={0: str(p)}))
correlations.append(g)
predictions.append(beta_results.assign(predictors=str(X_names[i])))
models.append(beta_models)
cor = pd.concat(correlations, axis=1).assign(outcome=y_name)
pred = pd.concat(predictions, axis=0)
mod = pd.concat(models, axis=0)
return cor, pred, mod
Adding in the function below completes the picture by calling r2_by_predictor on any number of outcomes.
def r2_by_predictor_and_outcome(data, predictors, outcomes, scale=True, cv=5):
if not isinstance(outcomes, (list, tuple)):
outcomes = [outcomes]
all_cor, all_pred, all_mod = [], [], []
for i, clf in enumerate(outcomes):
results = r2_by_predictor(data, predictors, y_name=clf, scale=scale, cv=cv)
cor, pred, mod = results
all_pred.append(pred)
all_cor.append(cor.reset_index()
.drop(columns='outcome')
.melt(id_vars=['fold', 'scorer'], value_name=clf, var_name='predictors'))
all_mod.append(mod.assign(outcome=clf))
all_cor = (reduce(lambda x, y: pd.merge(x, y, on=['fold', 'predictors', 'scorer']), all_cor)
.melt(id_vars=['fold', 'predictors', 'scorer'], var_name='outcome', value_name='$R^2$'))
all_mod = pd.concat(all_mod).reset_index(drop=True)
all_pred = pd.concat(all_pred).reset_index(drop=True)
return all_cor, all_pred, all_mod
Final notes
At some point I’ll throw these together in a public github (it’s in a private repo for an ongoing project at the moment) along with some more code for tests and running some of the more specific things I needed to do. I should also add that there are a lot of options for tweaking the setup in the betareg package, so you should check out the vignette for this.